You have probably heard of Base64 encoding, or seen it on the internet. In simple words, Base64 encoding is a way to transform binary data to printable, readable text (with ASCII characters). The name originates from the fact that only 64 characters are used to represent binary data!
In this post, you will learn how Base64 encoding works, and how to transform any binary data into a Base46 string that can be transported over text-transfer protocols. In addition, we will also learn how we can decode Base64 text with the inverse method.
This post assumes that you understand how binary works, and perhaps even hexadecimal to binary conversion and vice-versa. In addition, it may make things easier to understand if you also know what ASCII is.
Encoding Base64
As we’ve mentioned, Base64 gets its name because it only uses 64 ASCII characters to represent binary data. More specifically, you will only find the following characters in any Base64 encoded string:
\begin{align*}
&\texttt{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,} \\
&\texttt{Q,R,S,T,U,V,W,X,Y,Z,a,b,c,d,e,f,} \\
&\texttt{g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,} \\
&\texttt{w,x,y,z,0,1,2,3,4,5,6,7,8,9,+,/}
\end{align*}Clearly, the characters used are the English alphabet uppercase characters \texttt{[A-Z]}, followed by the lowercase ones \texttt{[a-z]}, followed by digits \texttt{[0-9]}, and finally, the characters \texttt{\{+,/\}}.
Essentially, Base64 encoding will turn any binary data into a sequence of the aforementioned characters. For example, the two bytes \texttt{\{11110011,10100000\}} will turn into the Base64 string “\texttt{86A=}“.
Interestingly, you might be wondering what the equals sign is doing in that string since we have stated that Base64 strings only have the characters above. Basically, the statement is half right: there may be padding equal (=) characters depending on the data encoded! We’ll talk more about it in the remaining character sections.
The following subsections will be explaining how to transform binary data into Base64 strings.
Algorithm For Base64 Encoding: The Full Picture
Taking into consideration a very high-level description of the Base64 encoding algorithm to keep things simple, and given an array (or sequence) of bytes, the following list describes how Base64 encodes the sequence of bytes.
- Split the byte sequence into groups of three bytes long partitions.
- For each group of three bytes, do the following:
- Concatenate the 3 bytes into one long sequence of 24-bits.
- Split the 24-bit long sequence into 4 groups of 6 bits.
- Use the value of each 6-bit group as an offset to the list of allowed Base64 characters.
- Transform each 6-bit group into a character from the Base64 character list with the offsets, preserving the order.
- If there are remaining bytes, or no full 3-byte groups at the end:
- Concatenate the remaining bytes.
- Split the concatenated bits into as many 6-bit groups as possible.
- For the remaining non 6-bit group, pad it with zeroes until you have a last 6-bit group.
- Convert each group into a Base64 character with the offsets from the 6-bit groups.
- Pad the resulting string for the remaining bytes with “=” until there are 4 characters altogether.
- Finally, put all the four-character groups together in order, and that’s the Base64 string for the input byte array.
Characters And Their Offsets/Positions In Base64
| Char | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
| Offset | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Char | Q | R | S | T | U | V | W | X | Y | Z | a | b | c | d | e | f |
| Offset | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| Char | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v |
| Offset | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 |
| Char | w | x | y | z | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | + | / |
| Offset | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 |
I know it seems difficult to understand the above at first. However, Base64 essentially considers groups of three bytes from the input and transforms those bytes into four printable characters from the table above. More importantly, each character is given by the offset that each 6-bit resulting group represents. The table above shows the offset for each Base64 character.
Concatenating Three Bytes
Firstly, let’s assume we have exactly three bytes to encode with Base64; explaining the core idea of Base64 encoding becomes much simpler, and we will look at the edge cases — where we may not have a list of bytes whose size is divisible by three — in the later section of this post.
Interestingly, the word “concatenation” simply means to link things together in a series. Therefore, this is exactly what Base64 does with each group (or partition) of three bytes from the array of bytes being encoded.
For simplicity sake, the example in this section assumes we have the array of bytes \{\texttt{01010101, 01010101, 01010101}\} to encode. As the result of concatenating these three bytes, we get the long 24-bit value \texttt{01010101 01010101 01010101 }.

Finally, it’s worth mentioning that to store the long 24-bit value shown in the image above, you need a data type capable of storing at least 24-bits. In addition, will need to correctly align each byte in the 24-bit value with bit-shift operations! More on this in the post about programming Base64.
Splitting The 24-Bit Base64 Value Into 6-Bit Groups
Following the concatenation of three-byte groups, we now need to work out the four Base64 characters for that byte group.
Unsurprisingly, this is done by firstly splitting the long 24-bit value into four 6-bit values, and then converting those 6-bit values into the equivalent character as shown in table 1.

Hence, for the previously considered example, the image above shows the 6-bit groups in order, the decimal conversion for each 6-bit group (which is the character offset in table 1), and finally, the Base64 character for each 6-bit group. Essentially, the byte array \texttt{01010101, 01010101, 01010101} gets encoded to “\texttt{VVVV}” in Base64.
In addition, I want to mention that this process is iterative. For example, if we had the byte array \texttt{\{01010101, 01010101, 01010101, 01010101, 01010101, 01010101\}}, then the resulting Base64 string would be “\texttt{VVVVVVVV}“.
What Happens When There Are Characters Remaining At The End?
Assuming that the input byte array to a Base64 encoder will always have a length that a multiple of three is good for explaining the main idea of the algorithm. However, mathematically speaking, the input byte array will fall into one of the categories below.
- The byte array’s length is divisible by three (no remaining bytes) – For example, the array \texttt{\{0x67, 0x6f, 0x6d, 0x65, 0x73, 0x73\}}. Unsurprisingly, we won’t have any remaining characters after the three-byte splits, so the method explained above can be carried out normally.
- There’s one remaining byte after the three-byte split – For example, \texttt{\{0x67, 0x6f, 0x6d, 0x65\}}, where we have \texttt{\{0x65\}} after splitting the first three bytes.
- There are two remaining bytes after the three-byte split – For example, \texttt{\{0x67, 0x6f, 0x6d, 0x65, 0x73, 0x73\}}, where we have \texttt{\{0x73, 0x73\}} after the three-byte split.
Basically, we’ve already seen the case where the input’s length is divisible by three. However, in the next subsections, we will see how Base64 handles each edge case with the remaining bytes after the split.
Two Remaining Bytes After The Three-Byte Split
When the length of the input byte array is a multiple of three plus two bytes, there will be two remaining bytes after the three-byte partition split. Specifically, this is true for any input array size of length 3n+2, such as byte arrays with lengths 2, 5, 209, and 1262.
Due to each byte having exactly 8-bits, the remaining two bytes can form a group of 16 bits. Expectedly, we concatenate those two bytes and split them into two groups of 6-bits and one group of 4-bits, preserving the order of concatenation.
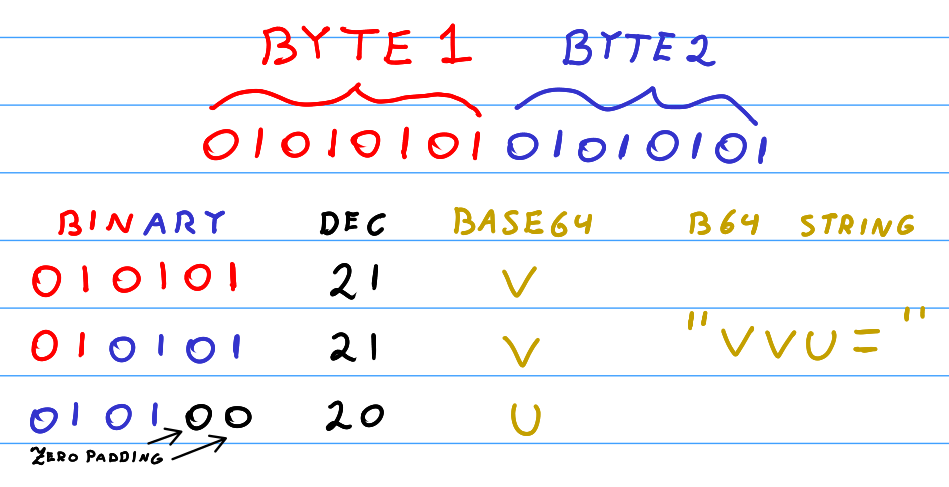
But how do we form the four required ASCII characters from the two bytes? Obviously, we can get two Base64 characters from the first two 6-bits in the same way as usual. Interestingly, the trick is padding the last 4-bit partition with two zeros, forming another 6-bit number which can then be used to get a third Base64 character!
However, we still have to get one more character to form the 4-character Base64 string. In addition, we have no more data left from the input array, so what do we do? We simply pad the string with the equals sign “=”. It feels like cheating, but it’s how Base64 makes sure that every group after the three-byte partition has exactly four characters – even the incomplete groups at the end! This is all illustrated in figure 3.
One Remaining Byte – The Last Edge Case
As you can probably guess, any input byte array of length 3n+1 will have one remaining byte at the end after the three-byte split.
Unsurprisingly, the process is almost the same as the two remaining bytes: we take the available bit data, split it into full groups of 6-bits, and pad the remaining with zeros.

Since there is only one byte of data, we can only form one full 6-bit group, then another group with the two remaining bits and four padding zeros, as shown in Figure 4. Unfortunately, even after the padding, we can only get exactly two Base64 characters from one byte, so we add two equals “=” signs at the end to create a full 4-character long Base64 string!
TL;DR: Summary Of The Base64 Encoding Algorithm
In summary, for any given input byte array, we first split the bytes into as many full three-byte partitions as possible. This may leave either two or one remaining byte at the end. Hence, for each partition of bytes, we obtain the equivalent Base64 string.
For the full three-byte partitions, we concatenate each partition into a long 24-bit value, then split this value into four 6-bit partitions. Finally, we convert each 6-bits into a Base64 character from table 1, using the 6-bit value as the character offset – the Base64 string is obtained by concatenating these characters together.
If there are two remaining characters, we concatenate them and create two groups of 6-bits and a group of 4-bits. Following that, we pad the last 4-bit group with two zeros, get the corresponding Base64 character for each 6-bit group and add one padding equals sign to end up with a four-character Bse64 string.
Last but not least, when there is a single byte left after the three-byte partition, we split that byte into one partition of 6-bits and one 2-bit partition. Similarly, we pad the last 2-bits with four zeros to make a full 6-bit partition, leaving us with two 6-bit groups. Finally, convert each 6-bit group into a character, add two padding equals signs at the end, and Bob’s your uncle.
Some Final Notes On The Base64 Encoding Algorithm
- For each three bytes in the input byte array to encode, Base64 converts them into exatcly four characters.
- For the remaining one or two characters that an input may have after the three byte split, the resulting Base64 string is also four characters long.
- If there were two remaining bytes, then the resulting Base64 string for the whole byte array will have one equals sign at the end.
- If there was one remaining byte, the resulting Base64 string will have two equal signs at the end.
- Due to the nature of the algorithm, for any given byte array as input, the resulting Base64 string will always have a length that is a multiple of 4!
Decoding Base64 Strings
Now that you (hopefully) understand how the base64 encoding algorithm works, decoding Base64 strings is really trivial: the intention is to do the opposite to encoding. In other words, we work out what three-byte values a group of four Base64 characters would represent.
Comparing to the Base64 encoding algorithm, decoding is very similar. More specifically, given a valid Base64 string, we first split it into partitions, decode each group individually into an array of three bytes. The decoded bytes are obtained by then joining all the decoded bytes together into a flat array.
In the upcoming subsections, we will talk about how to split a Base64 string, apply the decoding on each split partition, and finally, how to decode strings that have been padded with equals signs.
Splitting The Base64 String Into Four Character Partitions
Similar to encoding, the first step for decoding a Base64 string is to split the string into groups of four characters. Importantly,
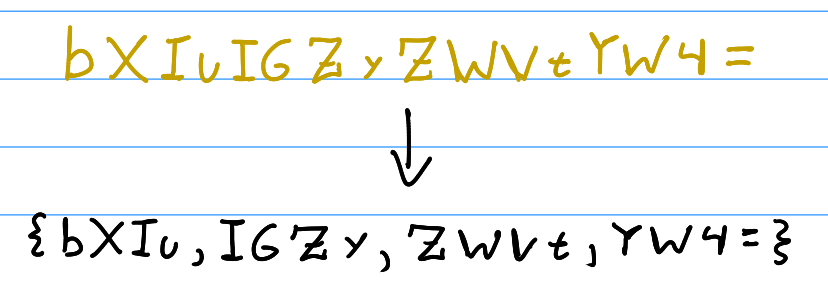
As you can see in Figure 5, the string \texttt{bXIuIGZyZWVtYW4=} gets split into four partitions of four characters long.
Interestingly, the example string above has one equals sign at the end of it, but generally, any valid Base64 string falls into one of the following categories:
- No equals sign.
- One equals sign at the end.
- Two equals signs at the end.
Furthermore, any valid Base64 string’s length is always divisible by four – any other string that doesn’t fall into the categories above is technically invalid Base64, however, we will talk about some exceptions at the end of the decoding section.
No Padding Equals – The Happiest Of Paths
When the four-character partition being decoded has no equal signs at the end, it means that there were exactly three bytes originally. For example, the first four-character partition of \texttt{bXIuIGZyZWVtYW4=} is \texttt{\{bXlu\}}, which has no equals sign.
As you can see in Figure 6, decoding the partition is just a matter of finding which position each character in the partition is in table 1 (or the offset of that character in the Base64 character array), concatenating all the offsets into a 24-bit value, then split the 24-bit value into three bytes.
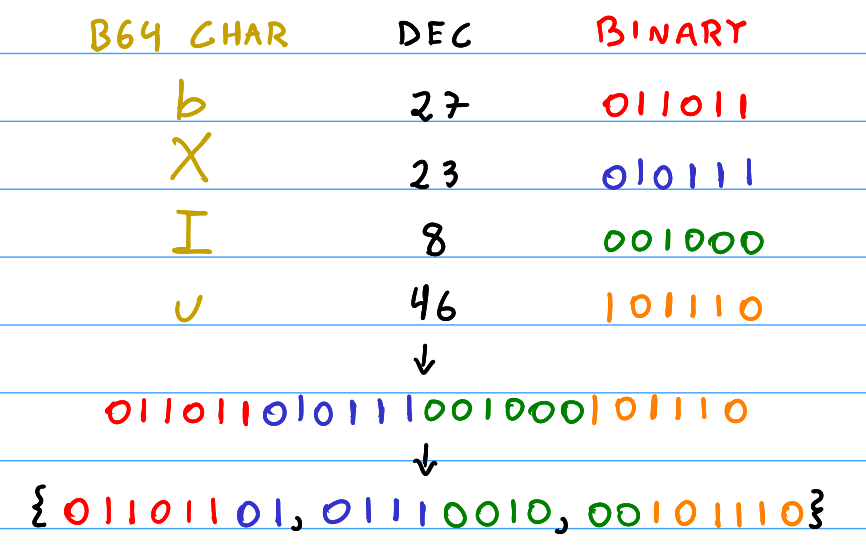
For example, for the partition \texttt{\{bXIu\}} as seen in Figure 6, the second character \texttt{X} has an offset of 23 (or binary value \texttt{0x17}) in the Base64 character array. Simply put, we do this for all the characters in a four-character group, then concatenate all the values and extract the three original bytes out, as seen in the figure above.
One Equals Sign – We Know There Were Two Remaining Bytes
Hopefully, you remember from the previous encoding section, if the encoding three-byte partition left a group of two remaining bytes, the generated Base64 string for those remaining bytes has an equals padding sign at the end. For this reason, the converse of this is also true: if a Base64 four-character partition has an equals sign, there must have been two original encoded bytes.
Importantly, since there were two original bytes, and we know that the Base64 characters were created from two full 6-bit values, and a 6-bit padded with two zeros, we can simply reconstruct the original bytes by removing the two padded zeros and remaking the two bytes. We can simply ignore the equals sign and just work with the three meaningful characters.
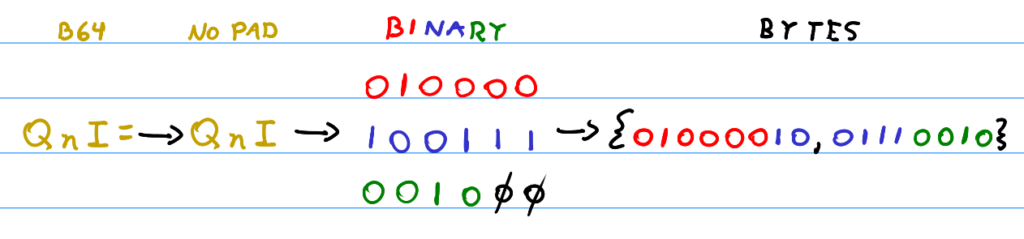
For example, for the Base64 string partition \texttt{YW4=}, we would simply get the offsets for each character in the string \texttt{YW4}, giving us \texttt{\{24, 22, 56\}} in decimal. Following that, converting these values to 6-bit binary, we would have \texttt{\{011000, 010110, 111000\}}. Concatenating these values into a long 18-bit value and removing the last two padding zeros, we get the 16-bit value \texttt{01100001 01101110}, and voilà – split this 16-bit value into two bytes, or the original bytes.
One Byte Remaining Means Two Equals Signs
Basically, when there are two equals signs at the end of a Base64 string partition, we know that there must have been one original byte. For this reason, if you ignore the two equals signs at the end, you can reconstruct the original byte in the same manner as the previous section, when there’s only one equals sign.
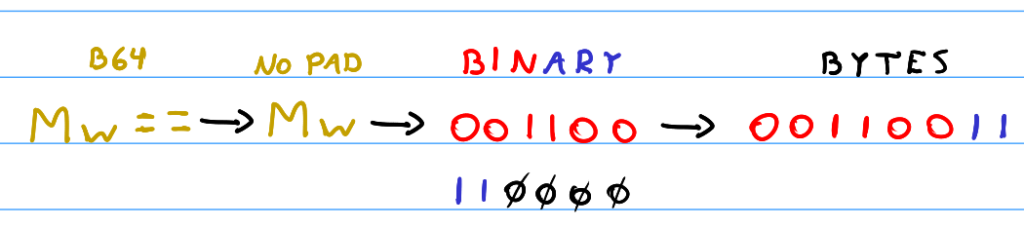
The only difference, of course, is that we know we should have one full 6-bit value and one 6-bit value padded with four zeros. Therefore, after concatenating the 6-bit values, we remove the last four zeros, leaving us with the single, original byte!
For example, for the Base64 string partition \texttt{QQ==}, we ignore the equals sign and get the offsets of each character in table 1, leaving us with offsets \texttt{\{16, 16\}} in decimal. Converting to binary and consequently removing the last four zeros, we have \texttt{\{01000001\}} – the original byte.
What Do We Do With Invalid Strings?
Understanding the above sections and being able to apply the decoding ideas to any Base64 string means you can encode and decode any arbitrary binary data. However, what happens when we get an odd-looking Base64 string to decode? What if the Base64 string we have does not have a length that is divisible by four?
Quite simply, if the string we are given does not have the length divisible by four and does not fall into any of the categories stated in the previous section, it is not a valid Base64 string.
Nevertheless, I have seen cases of decoders who decide to ignore certain irregularities in certain invalid strings. For example, the string \texttt{QQQQMw===} is clearly not a regular Base64 string as it has more than two padding equal signs. However, some decoders decide to ignore the remaining “=” signs after the four-character split, essentially just considering the groups \texttt{\{QQQQ, Mw==\}}.
Furthermore, it’s worth noting that any string with invalid characters — such as characters not shown in table 1 — is flat-out invalid, and attempting to decode them will fail. In the same category, we can also say that any string that has the last four-character partition with three padding “=” (equals) signs is invalid, as this is literally impossible to have been generated from the encoding algorithm.
In conclusion, there may be certain strings that we can consider decoding even if they are invalid. However, there are certain strings that cannot be decoded even if we try and hack them.
TL;DR Summary Of Base64 Decoding
To summarise, decoding a valid Base64 string is very similar to encoding. Firstly, we split the string into groups of four characters, and there should be no remaining characters if the string is valid!
We then work out the offset of each character per group, whose value in the 6-bit binary is then used to create the long 24-bit value, and then split this value into the three original bytes.
If the Base64 four-character group has padding equal signs, you will need to consider fewer 6-bit groups and remove the padding zeros from the offset bits. One padding equals sign means you will have three 6-bit groups and need to discard two bits from the last group. Similarly, two padding signs mean you will have two 6-bit groups and need to discard four bits from the last group before concatenation.
Have I missed anything? Have you spotted any typos or errors in the post? Got useful feedback? Feel free to comment below!
This post is part of a series about understanding popular concepts. Check out the last post about understanding the trapezium rule!
Be First to Comment