Base64 encoding is an easy binary-to-text encoding scheme. It’s used in various places: from encoding bytes for sending over the internet, to storing public/private keys in text format. In this post, we look at how to Base64 encode and decode in modern C++20!
Understanding Base64 Encoding & Decoding
Base64 can be quite tricky to understand if you’re not used to working with binary data, but luckily for you, I posted a comprehensive tutorial on how Base64 encoding and decoding work.

Check out the post and make sure you understand the overall algorithm, as this post assumes you understand Base64 and how the bit operations help you transform binary into text. In addition, the pretty hand-drawn illustrations may help you visualise the whole process!
Requirements For This Project
Before we get into the technical details, let’s look into what we need to build the modern C++ Base64 encoder.
Firstly, the code shown in this post contains C++20 features such as std::span, as well as C++17 features like if initializers and std::optional. For this reason, you need a fairly recent compiler and a not-so-old version of CMake (perhaps at least 3.16). From the compiler support cppreference page, you need at least the following compiler versions:
- GCC version 10.
- Clang version 7.
- MSCV version 19.26.
Finally, to build the entire project, you will need the Conan C++ package manager and Github to pull the code locally. There will be more on this in the following section about where to find the code.
Base64 Encode With Modern C++
In this section, we look at how to implement a safe Base64 encoder using a simple encoding table. Long story short, we consider three bytes each time, concatenate their values, and split them into four ASCII characters according to the encoding table – this is outlined in more detail in the aforementioned Base64 tutorial.
Using Arrays To Store The Encoding Table
Ideally, once we’ve split the three bytes into four six-bit values, we need to convert these values into a Base64 character. For a six-bit value, the resulting character is the one at the position given by the six-bit value in the following Base64 character array:
\begin{align*}
&\texttt{A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,} \\
&\texttt{Q,R,S,T,U,V,W,X,Y,Z,a,b,c,d,e,f,} \\
&\texttt{g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,} \\
&\texttt{w,x,y,z,0,1,2,3,4,5,6,7,8,9,+,/}
\end{align*}For example, for the six-bit value \texttt{000000}, the character would be the one at position zero, or \texttt{"A"}. Likewise, the character for \texttt{111111} would be \texttt{"/"}.
But how can we represent the table above in C++? If you think about it, the table above is simply a contiguous array of characters, where each element is laid out as per the table. Without further ado, the following array represents the encoding table we outlined in this section.
std::array<char, 64> constexpr encode_table{
'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K',
'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V',
'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd', 'e', 'f', 'g',
'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r',
's', 't', 'u', 'v', 'w', 'x', 'y', 'z', '0', '1', '2',
'3', '4', '5', '6', '7', '8', '9', '+', '/'};
You can see we have exactly 64 characters, and the order of the characters matches the encoding table we discussed previously – we will later use this array to convert the six-bit values to Base64 characters!
Finally, the code snippet above requires you to include the <array> header.
How To Encode A Full Byte-Triple
“Three is a magic number. It takes three legs to make a tripod or to make a table a table stand” – Similarly, it takes three characters to convert from binary to Base64, and three-character splits are fundamental to the algorithm.
For this reason, if we can encode a chunk of three bytes, we can encode an entire array of bytes using padding tricks we will see later.
std::array<char, 4> encode_triplet(std::uint8_t a, std::uint8_t b, std::uint8_t c)
{
std::uint32_t const concat_bits = (a << 16) | (b << 8) | c;
auto const b64_char1 = encode_table[(concat_bits >> 18) & 0b0011'1111];
auto const b64_char2 = encode_table[(concat_bits >> 12) & 0b0011'1111];
auto const b64_char3 = encode_table[(concat_bits >> 6) & 0b0011'1111];
auto const b64_char4 = encode_table[concat_bits & 0b0011'1111];
return {b64_char1, b64_char2, b64_char3, b64_char4};
}Unsurprisingly, function encode_tripletin the code snippet above will do just what we expect: given three bytes represented by a, b, and c, it will return four Base64 characters.
For the purposes of this post, I chose std::uint8_t to represent a byte, and this definition can be found in the header <cstdint>. In addition, for concatenating the bytes in line 3, we use the type std::uint32_t as the results will be exactly 24-bits, so 32-bits should be enough to hold it.
Going From Bytes To Base64 Characters
As you should know by now, the overall goal of Base64 encoding is to transform some bytes into a string of characters contained in the encoding table. Furthermore, I mentioned that each resulting character is the equivalent offset of a value in the encoding table.
Let’s suppose that the variable concat_bytes in the snippet above is a 24-bit value, which we obtained from concatenating bytes a, b, and c from left to right. In fact, concat_values is actually a 32-bit value containing those three bytes concatenated, plus zeroes on the eight left-most bits.
Interestingly, how can we split that 24-bit value in concat_bytesinto four 6-bit values? To make the problem a bit simpler, let’s suppose you want the second 6-bit value.
auto const concat_bytes = ... ; // 24-bit long value
auto const second_six_bits = (concat_bits >> 6) & 0b0011'1111;In the snippet above, the variable second_six_bits holds the second six-bit values, by firstly shifting all the bits of concat_bits to the right six times and masking the first six-bit values.
In more detail, the bit shift operation will put the bits \texttt{[11-17]} (inclusively) in the positions \texttt{[0-7]}. In addition, the masking with & 0b0011'1111 has the effect of only keeping the values in the first 6-bits, zeroing out all the other bits in the shift operation.
Essentially, these two operations simply store the second 6-bit value as an integer value in second_six_bits. Due to masking the first six-bits, the integer value will never be anything outside the range \texttt{[0, 63]}. This same technique is used to get the first, second, third, and fourth six-bit values in the 24-bit, so we can use them for the character offsets!
Converting A Six-Bit Bit Value To A Base64 Character
Being able to convert the three bytes into four six-bit values is half of the work, and the other half is simply turning each six-bit value into a Base64 character.
Interestingly, this is where the encode_table comes in! Long story short, the six-bit values represent the offset of the Base64 characters in the encoding table.
// get the six_bit value with the bit operations
auto const a_six_bit_value = ...;
// use the six_bit value as the character index
auto const base64_char = encoding_table[a_six_bit_value];In the code snippet above, base64_char contains the character represented by the six-bit value. Needless to say, there’s nothing very interesting going on here, we are simply indexing into the encoding table array.
Importantly, the code above should be safe if a_six_bit_value is always in the range \texttt{[0, 63]}, because if it’s outside that range, you will be accessing invalid memory as the encoding table only has 64 characters!
Finally, this technique is used for getting all the four characters for every three bytes of the data to encode.
What Happens When We Don’t Have Three-Bytes In The Input To The Base64 Encoder?
How long is a piece of string? Like strings, byte arrays can have any size, however, we do know some facts about these sizes:
- A byte array’s size could be exactly divisible by three such as 0, 3, and 333.
- The size of an array could be a multiple of three plus two remaining characters. For example, array sizes of 2, 11, or 554. Essentially, if we split byte arrays of these sizes into groups of three, there would be two remaining bytes at the end.
- Lastly, if the array’s length is a multiple of three plus one — such as 1, 10, 1000 — we would have one remaining character after partitioning the array into groups of three.
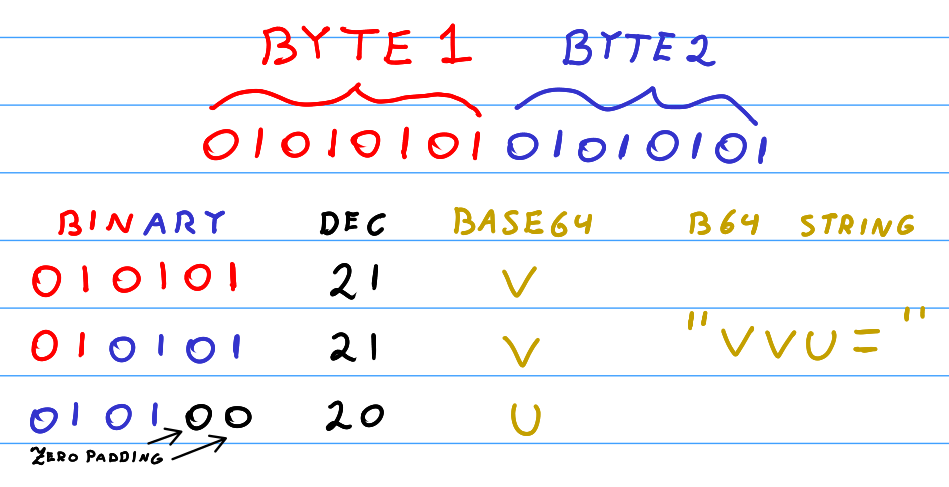
But how do we deal with the cases where we have remaining characters after the three-byte partition? Basically, we pad the last group (either two or one byte) with zeros, carry out the three-byte encoding, and pad the resulting Base64 string with = values. I’d highly recommend reading about these edge cases in my post on understanding Base64 encoding and decoding.
Encoding The Remaining Two Bytes
Let’s assume that you partitioned your bytes into groups of three, but the final group only has two bytes in it. Ignoring the final incomplete partition, you encoded all of your perfect three-byte groups and appended them into the Base64 encoded string base64_result. How do we then encode the final, incomplete group of two bytes according to the Base64 specification?
Mathematically speaking, we can simply pass the two remaining bytes into the encode_triplet function, setting the last input character as a 0. Following that, we simply ignore the last character in the result, appending only the first three returned Base64 characters into base64_result, and finally, append a = to it as well.
std::uint8_t const final_byte1{0x98};
std::uint8_t const final_byte2{0x98};
auto const base64_chars = encode_triplet(final_byte1,
final_byte2,
0x00);
std::copy_n(begin(base64_chars),
3,
back_inserter(base64_result));
base64_result.push_back('=');And just like that, we have encoded the last two-byte partition and added it to our result.
Encoding The Remaining Single Byte
Hopefully, by now, you got the gist of this. Similarly to the two remaining bytes case, we simply pass the single remaining byte into encode_triplet, and the remaining byte arguments will both be 0.
std::uint8_t const final_byte{0x98};
auto const base64_chars = encode_triplet(final_byte1,
0x00,
0x00);
std::copy_n(begin(base64_chars),
2,
back_inserter(base64_result));
base64_result.push_back('=');
base64_result.push_back('=');Another difference is that we now add an extra = padding character to the result.
Decoding Base64 Strings In C++
“Nothing is invented, for it’s written in nature first everything is copied and reused” – Me twisting a famous quote… But it’s true, most problems are just a different form of other problems. This is no different in Base64: decoding is just “encoding” Base64 characters into bytes. So the solution will be fairly similar to encoding.
It will all be clearer when we look at the decoding table. More precisely, we have the following problem: for a given Base64 character, what six-value did it originally have?
In this section, we present similar ideas to Base64 encoding, after all, it’s the same problem except we’re doing the opposite! Specifically, we will use a decoding table to get six-bit values for each character, and also bit-shift operations to reconstruct the original bytes.
Decoding Base64 Strings: The End Game
Briefly speaking, Base64 decoding a valid string involves splitting the string into partitions of four Base64 characters. Following that, we transform each four-character partition into the original three bytes, and when we add all those bytes to an array in order, we get the decoded bytes.
Importantly, the method described in this section assumes that the input to the decoding function is always valid, but this is not always the case. For this reason, we must always check that the input string is a valid Base64 string, and you can see this in the full code:
- Check that the length of the string to decode is always a multiple of 4.
- All characters in the input string need to be valid Base64 characters, it cannot contain characters that aren’t in the
encode_tablearray. - Last but not least, the last four-character group may contain at most two equal padding signs at the end.
Using A Decoding Table To Find Six-Bit Values For a Character
If we want to reconstruct the original bytes for the string \texttt{AAAA}, we need to get the six-bit value for the character \texttt{A}, which would be \text{000000}.
std::array<std::uint8_t, 128> constexpr decode_table{
0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64,
0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64,
0x64, 0x64, 0x64, 0x64, 0x64, 0x3E, 0x64, 0x64, 0x64, 0x3F, 0x34, 0x35, 0x36, 0x37, 0x38, 0x39, 0x3A, 0x3B, 0x3C,
0x3D, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x64, 0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0A,
0x0B, 0x0C, 0x0D, 0x0E, 0x0F, 0x10, 0x11, 0x12, 0x13, 0x14, 0x15, 0x16, 0x17, 0x18, 0x19, 0x64, 0x64, 0x64, 0x64,
0x64, 0x64, 0x1A, 0x1B, 0x1C, 0x1D, 0x1E, 0x1F, 0x20, 0x21, 0x22, 0x23, 0x24, 0x25, 0x26, 0x27, 0x28, 0x29, 0x2A,
0x2B, 0x2C, 0x2D, 0x2E, 0x2F, 0x30, 0x31, 0x32, 0x33, 0x64, 0x64, 0x64, 0x64, 0x64};
In the snipped above, the decode_table byte-array solves that problem. If you have a single valid Base64 character, such as \texttt{A}, then using that character as the index to the array will give you the original six-bit value.
As an example, decode_table['A'] will return 0x00. Similarly, using other characters as the index for the decode_table array gives you the original six-bit offset of the encoded character.
Decoding Four Base64 Characters With No Padding
Assuming we have a perfectly valid four-character partition of a Base64 string, the following function decode_quad decodes the four characters given as inputs.
std::array<std::uint8_t, 3> decode_quad(char a, char b, char c, char d)
{
std::uint32_t const concat_bytes =
(decode_table[a] << 18) | (decode_table[b] << 12) |
(decode_table[c] << 6) | decode_table[d];
std::uint8_t const byte1 = (concat_bytes >> 16) & 0b1111'1111;
std::uint8_t const byte2 = (concat_bytes >> 8) & 0b1111'1111;
std::uint8_t const byte3 = concat_bytes & 0b1111'1111;
return {byte1, byte2, byte3};
}
For example, for the four-characters \texttt{AAAB}, calling decode_quad('A', 'A', 'A', 'B') would return the vector containing {0x00, 0x00, 0x01}.
How is this achieved? Mostly with the decode_table. Essentially, we get the original six-bit values for each character and place each value in their respective original place in a 32-bit integer. Although we don’t use all of the 32-bits, the 24 least significant bits will contain the original concatenated bytes (refer to the encoding section).
Finally, the original three bytes are acquired by getting the first eight bits, then the second and third eight bits from the concatenated six-bit values.
Figuring out how this is all achieved with bit-shift and masking operations is left as an exercise to the reader ~~ I’ve always wanted to say this 🙂
What If The Last Group Of Characters Has Equal (=) Padding Characters?
Ideally, you need to iterate over each partition of four characters, decode each of them and append every three bytes returned by decode_quadto a byte array. However, this only works if the encoded string has no padding at the end of it.
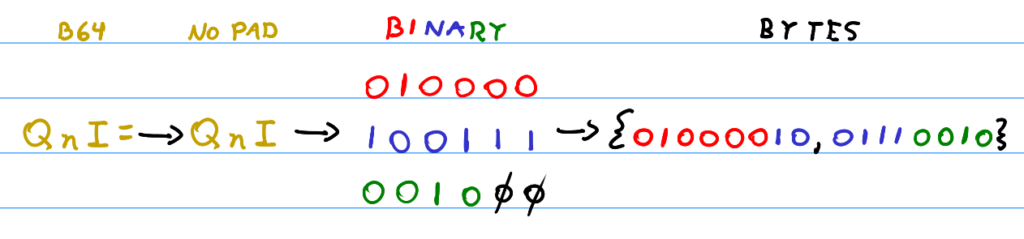
For the decoding to work with any valid Base64 string, we would need to do something special to the last partition of four characters if they have padding:
- If the partition only has one
=(equal) sign at the end, we simply calldecode_quad(a, b, c, 'A')witha,b, andcas the first, second and third characters of the group, respectively. Importantly, we only append the first two bytes returned from this call to the result byte-array. - If the parition has two
=(equal) signs at the end, we calldecode_quad(a, b, 'A', 'A')where ‘a’ and ‘b’ are the first and second characters of the last parition. Similarly, we only append the first character returned from the call to the return byte-array.
Without baffling too much, you can see how this is done in the full code on Github. The function in question here is base64::decode.
Base64 C++ Encoder And Decoder On Github
Without further ado, you can view all the code for the Base64 encoder in this Git repository. If you want to build it, follow the instructions in the README.md file.
Most of the code was shown and explained in this post, but you can see the whole picture in the Github repository. More precisely, the two main functions are base64pp::encode(...)and base64pp::decode(...) – the input checking and the overall logic for encoding and decoding are here.
Moreover, here’s an overview of the project structure:
- “base64pp/include/base64pp/base64pp.h” is the header file declaring the
base64pp::encodeandbase64pp::decodefunctions. - “base64pp/base64pp.cpp” defines the encoding and decoding functions, all the program logic can be found in this file.
- “base64pp/CMakeLists.txt” is the CMake file that defines the
base64pplibrary. - “base64pp/tests/base64pp_tests.cpp” defines the unit tests for the encoder and decoder.
- “tests/CMakeLists.txt” defines the test executable
base64pp_tests, which usesGTestsas the unit test framework.
If you’re not quite comfortable with CMake, I recommend checking out my posts on how to create libraries with CMake and adding include directories to targets with CMake.
What’s The Point Of This Post? Aren’t There Many Base64 Encoders Out There?
I decided to write this post after being frustrated with the quality of some Base64 encoders out there. For example, Googling “C++ Base64 Encoder” will either land you on a StackOverflow thread or this Github Base64 encoding gist.
Although I have nothing against the writers of the demo code in those threads, both the top answers on Google are very bad examples of Base64 encoding in C++. Not only are the snippets unmaintainable due to poor readability, but I’ve also spotted several serious issues with the top examples:
- C++ undefined behaviour use, meaning that certain features these exmaples rely on aren’t actually guaranteed by the standard.
- Buffer overflows with certain input data, which can cause serious security-related issues.
- Lack of input sanity checks, allowing users to, for example, decode any invalid string.
- Very difficult to reason about the code as the examples seem to focus on solving the problem with the least number of lines. This isn’t always a good idea and it hurts the readibility of the code.
What’s worse is that I’ve seen these examples been copied and pasted into places they should never have. Very few of the examples I see on the first page of Google are actually production-worthy.
Stick To Already Tried-And-Tested Libraries Whenever Possible
Ideally, if there’s is a library that provides the functionality you need, then use it instead of reinventing the wheel! Similarly, if your project requires a Base64 encoder/decoder, your best bet is to use a popular library like OpenSSL to do that work.
Although third-party libraries can also have issues, it’s less likely that a widely tested and used library will do a worse job than the code you implement.
Knowing how it works under the hood is a bonus – in case you do spot issues with popular open-source libraries, you can fix it yourself! In fact, one of the projects I’ve worked with used an old version of OpenSSL where the decoding function was crashing; turns out it wasn’t properly checking invalid inputs and crashing on such inputs!
Have I missed anything? Have you noticed any errors or typos? Do you have useful feedback? Feel free to comment below!
Be First to Comment