John Conway was a very active British mathematician and authored several research papers on topics like numbers and group theory. His most well-known invention, perhaps not so mathsy, is the “Game Of Life” – a two-dimensional cellular environment, where each cell obeys a short list of rules.
It may not be the first time you come across the Game Of Life, in fact, it’s very popular among coders. I’ve actually been tasked to implement parts of the game in previous jobs interviews for well-known companies!
Moreover, this post is part of my Python implementations series, where we previously looked at topics such as implementing the trapezium rule in Python.
In this post, we will outline the rules of the game, look at how the rules change the state of the cells, and how complicated (yet interesting) structures can be made with only three rules!
Rules Of The Game Of Life – Simplicity Creates Complexity
The rules of the game of life model the growth of the cell population in a grid. Under population, overcrowding, and birth are the three concepts modeled in Conway’s Game Of Life, with the following rules:
- Under population: any alive cell with less than two neighbours will die in the next iteration.
- Over population: any alive cell with more than four neighbours will die in the next state of the game.
- Birth: any dead cell with exactly three neighbours will become alive in the next iteration of the game.
Interestingly, these three rules are the entirety of the Game Of Life! As you can probably guess, the intention of the game is to simulate evolution through simple rules that model how cells should behave.
Examples Of Cell Behaviour In The Game Of Life
Before this post gets way too technical, let’s look at some examples of how cells behave in the three rules mentioned above.
Contextually, the Game Of Life only requires a single input: the state of the initial grid. In other words, the only input to the game is a list of the cells that start off alive, the future iterations of the game rely on the first input.
Underpopulation Examples
When a region doesn’t have enough workers to exploit the resources of an area efficiently and support the wider population, the region is said to be underpopulated. Conway modeled this concept by stating that, in the Game Of Life, cells that have less than two neighbours will die.
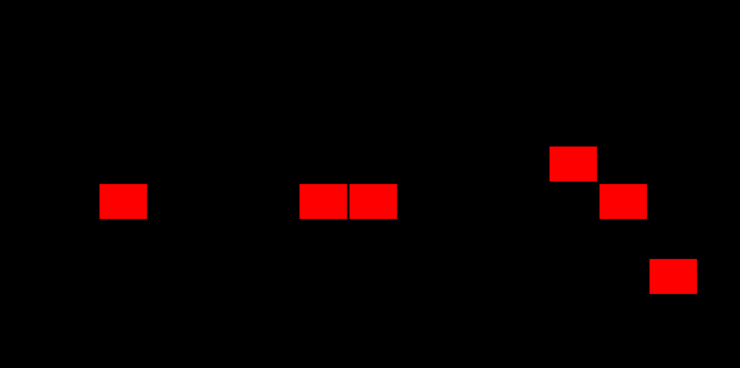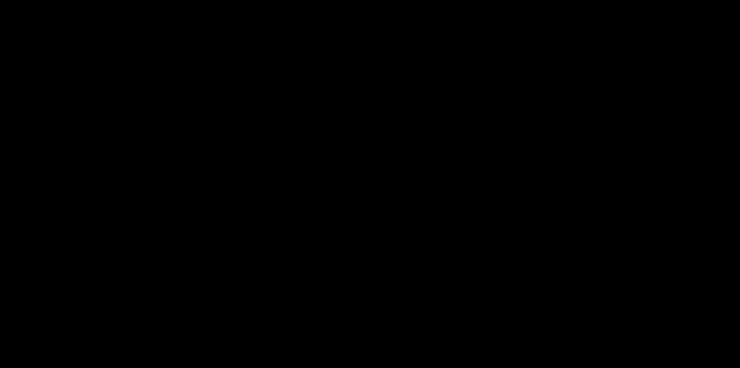
The figure above shows the effect of that rule in certain scenarios in the Game Of Life. Interestingly, finding an analogy to this concept in the real world is quite difficult; the human population has grown exponentially pretty much everywhere in the last century or so, hence most places are actually overpopulated!
Overpopulation Examples
Have you heard of Hong Kong? How about Mumbai? Or perhaps even São Paulo? These places are all overpopulated. In simple terms, overpopulation means that there are too many inhabitants using the resources of a particular area.
As a result, issues like poverty, pollution, and poor quality of life may arise in overpopulated places. Conway’s modeled this idea in the Game Of Life by having cells dying off when they have more than three live neighbours.

The gif above shows a fairly popular oscillator in the Game Of Life. As you can see, the corner cells die out as each of them have exactly four alive neighbours. In the following iteration, they respawn as those cells have exactly three neighbours each.
Cell Birth Examples – Generating Data
Well, no analogies are needed here. We should all be fairly aware of what “birth” means. More specifically, Conway modeled this idea by having dead cells become alive when they have exactly three alive neighbours.

Admittedly, I struggled to find a simple initial setup that would only have cell birth in its iterations. For this reason, the gif above, which shows a lot of cells being born, also has cells dying due to other rules.
Structures To Represent The Game Of Life
Without further ado, we will begin to talk about the implementation. In this section, we will analyse the Python structures that represent the Game Of Life.
An easy way to get into the right mindset for this task is by throwing away all the complexity of the problem — in this case, the Game Of Life — and think about the data implied by the problem’s statement.
So since the Game Of Life is a cellular automation system (assumed to be a two-dimensional grid in this post), we need a way of representing cells in a grid. More precisely, we want to represent cells that are either alive or dead.
Programatic Representation The Game Of Life
At its core, the Game Of Life is a two-dimensional grid, where each cell is dead or alive.
Naively, we could create a Python class to encode the Game Of Life structures. Something like the following example.
class GameOfLife:
def __init__(self, width, height, initial_cells):
self.width = width
self.height = height
self.initial_cells = initial_cellsBut the above is essentially just a tuple containing the dimensions and the initial state of the board (cells). In addition, for the sake of simplicity, we define the board size so we can show the cells in the given range.
To make things simpler, we can just think of the structure above as a Python named tuple, with the dimension and the cells. The snippet below shows this idea.
from collections import namedtuple
Dimension = namedtuple("dimension", ["width", "height"])
GameOfLife = namedtuple("GameOfLife", ["dim", "cells"])So basically, we have a tuple type, with named arguments for the dimensions and the cells. Creating an object of this type is easy, something like the following line of Python will do.
grid = GameOfLife(Dimension(50, 50), some_list_of_cells)
How To Represent The Game Of Life Cells Programatically
You may have noticed that, in the representation of the Game Of Life grid, we didn’t actually specify how each cell will be represented. You can probably think of a couple of different ways to represent the cells, so I wanted to talk about the advantages and disadvantages of different implementations.
Using Lists Of Booleans To Represent The Game Of Life Cells
Naively, we all probably thought about using a big list of booleans (either True or False values) to represent all the cells. True means that a particular cell is alive, and False means it’s dead. For illustration purposes, the code may look something like the following.
N_CELLS = 100*100
cell_list = [False] * N_CELLS
grid = GameOfLife(Dimension(100, 100), cell_list)However, having a one-dimensional list means that, for a particular cell with position (x,y), you will need to work out the position in the list. For this reason, this particular implementation brings extra logic and complexity to the overall implementation of the Game Of Life. It’s worth mentioning that, if you have a (1000,1000) grid but only a single cell alive, you will still be using all the memory that a (1000, 1000) grid would take, so it’s wasteful.
Can we not solve this issue by using a two-dimensional list? Indeed, if we use a list of lists of boolean, where every element in the outer list is itself a list of booleans representing each row, then you might simplify the logic a little. However, you will still have the memory waste issue.
Using Dictionaries/Maps To Record A Cell’s State
If we address the memory waste issue with lists, a step towards a better implementation would be to use maps. In this scenario, a viable solution is to use Python’s defaultdict type, where the keys are the (x, y) position tuple of a cell and the, and the values would be a boolean indicating whether or not the cell is alive. Specifically, the code could look something like the following block.
from collections import defaultdict
from collections import namedtuple
Cell = namedtuple("Cell", ["x", "y"])
some_cells = defaultdict(bool)
# cell at (1,2) is alive
some_cells[(1,2)] = TrueIt’s worth noting that defaultdict was picked over normal dictionaries because it creates a default value if the key is not in the dictionary. More specifically, the argument to defaultdict‘s constructor is the function that creates the default value. Hence, bool is our factory function, so when a key (or cell, in this case) isn’t in the dictionary, the value returned from the query will be bool(), or False.
In addition, there’s still some waste with that structure. Specifically, we only really care when a particular cell is present in the dictionary and its value is True. Moreover, defaultdict adds keys that were not previously in the dictionary if queried. In the example above, some_cells[(10,10)] would return False, but (10,10) will now be part of the dictionary with the default value.
As we can see, a dictionary can temporarily solve some of the issues with lists in this use case. However, it would be nice if could check if a cell is present in the dictionary and it’s value is True, in other words, a membership check. Can other data structures help us here?
Sets To Store Cells That Are Alive In The Game Of Life
If you thought of Python’s set data structure, you can pat yourself on the back.
Interestingly, elements are either in a set or not. For the Game Of Life, we can simply store the cells that are alive in the set.
cells = set()
# add cell at (1, 1), making it alive
cells.add(Cell(1, 1))
# create the game of life grid with the
# initial cells
grid = GameOfLife(Dimension(10, 10), cells)With this implementation, to check if a cell is currently alive, we can simply use the in operator. On the other hand, to kill off a cell we simply need to remove the cell from the set.
# create the initial cells with (1, 1) and
# (2, 1) being alive
>>> cells = set([Cell(1, 1), Cell(2, 1)])
# check if a cell is alive
>>> Cell(2, 1) in cells
True # (2, 1) is alive
>>> Cell(3, 1) in cells
False # (3, 1) is dead
# remove a cell
>>> cells.remove(Cell(2, 1))
>>> cells
{Cell(x=1, y=1)}
>>> Cell(2, 1) in cells
False # (2, 1) no longer aliveIt may not be apparent yet, but using a set simplifies the logic quite a bit. Determining whether a cell is dead or alive is a simple membership check.
In addition, there’s no more waste here. We only store the cells that are alive, so if your 1000x1000 grid only has one cell alive, the set will only have one element.
Essentially, we implemented a sparse boolean grid with this approach. If you have used Numpy or Scipy before, this approach is very similar to the sparse matrices in those libraries. Needless to say, this is the implementation I chose.
Applying The Rules Of The Game Of Life
Previously, we talked about the rules in Conway’s Game Of Life, and how a set of basic rules can create very complex behaviour in the two-dimensional cell grid. In this section, we will be looking at how the rules of the Game Of Life were applied using Python.
Admittedly, I made heavy use of Python’s list comprehensions and set comprehensions. For this reason, I recommend learning those concepts if don’t already know them.
Counting Dead And Alive Neighbour Cells
Hopefully, you realised that all of the rules in Conway’s Game Of Life depend on one thing: the state of the neighbouring cells. For this reason, it’s very important to be able to analyse the neighbour cells for every cell that is alive on the grid. The list below summarises the information we need for each Game Of Life iteration.
- For each cell that is alive, we need to find out how many neighbour cells are also alive.
- For each dead cell, we need to know how many neighbouring cells are alive.
Moreover, we only care about counting alive neighbours for dead cells that are themselves, neighbours, to live cells. I’ll let you figure out “why”.
Therefore, we will be looking at how we can count the number of alive neighbours for each cell that is currently alive, as well as dead cells that could possibly become alive.
Sets To The Rescue – Partitioning Neighbours Into Dead And Alive Categories
Hopefully, by the end of this section, you will realise how sets make our lives easier when finding all the concerned dead and live cells.
The idea is very simple: given a live cell in our grid, and all its possible neighbours, we know that each neighbour is either dead or alive. For example, the code below shows how we can return a tuple of (alive, dead)cell sets for each cell in our grid.
from collections import namedtuple
Neighbours = namedtuple("Neighbours", ["alive", "dead"])
def get_neighbours(grid: Grid, x: int, y: int) -> Neighbours:
offsets = [(-1, -1), (0, -1), (1, -1), (-1, 0),
(1, 0), (-1, 1), (0, 1), (1, 1)]
possible_neighbours = {(x + x_add, y + y_add) for x_add, y_add in offsets}
alive = {(pos[0], pos[1])
for pos in possible_neighbours if pos in grid.cells}
return Neighbours(alive, possible_neighbours - alive)Firstly, we did introduce a new type Neighbours that is essentially used to represent a tuple of (x, y)position sets. Its attributes, “alive” and “dead”, each represent neighbouring cells in each state. Note: every neighbour of a cell will be in either one of those states (“dead” or “alive”), but not both!
Transforming The Neighbour Sets Into Useful Information
Finally, to get the relevant cell information to apply the rules, we simply need to follow these steps:
- Create an empty dictionary, where the keys are
(x,y)positions of dead cells, and values are the number of live neighbours to it. This will be used to count how many live neighbours a dead cell has. - For each cell in our live cell set:
- Store the dead and live neighbours in variables using
get_neighbours(grid, x, y). - For each dead cell in the “dead” neighbour set, update the values in the dictionary we created earlier. Essentially, we will add one to the value of each
(x, y)cell that appears as a dead neighbour to a live cell, implying that dead cell has an extra live neighbour.
- Store the dead and live neighbours in variables using
And voilà! You now have all the information needed to implement all the rules. Particularly, we have the number of live neighbours for each live cell, and the number of live neighbours for dead cells that can become alive.
Updating The Game Of Life Grid
As you probably know by now, each iteration of Conway’s Game Of Life depends on the previous state of the cells. In other words, we need to know which cells were alive in the previous state so we can apply the rules for the next evolution.
For this reason, in each update of the game, we create a new Grid by deep copying the previous grid with Python’s deepcopy function. This allows us to modify the new Grid representing the new evolution without modifying the previous set of Cells.
from copy import deepcopy
old_grid = Grid(Dimension(10,10), {Cell(1,1)})
# New grid with the same contents as old_grid
new_grid = deepcopy(old_grid)
# Modifying new grid won't modify the previous
# grid
new_grid.cells.add(Cell(1,2))Interestingly, without the deepcopy, I found that Python would shallow copy the Cell sets. Consequently, this means that, when a new cell is added or removed from the new Grid, the previous grid would also change, affecting the rules and producing unexpected results.
Supposedly, this is due to Python’s rules on the mutability of objects, but I am not too sure. Perhaps you can drop a comment explaining why this happens (shallow copy of the member set variable)!
Implementing {Over, Under}population And Birth Rules Of Conway’s Game Of Life
Assuming we have the old and new Grid objects, the following code implements the overpopulation and underpopulation rules. In addition, the cell birth rule is also implemented as we have all the information outlined in the cell information algorithm section.
new_cells = deepcopy(old_grid.cells)
undead = defaultdict(int)
for (x, y) in grid.cells:
alive_neighbours, dead_neighbours = get_neighbours(old_grid, x, y)
if len(alive_neighbours) not in [2, 3]:
new_cells.remove((x, y))
for pos in dead_neighbours:
undead[pos] += 1
for pos, _ in filter(lambda elem: elem[1] == 3, undead.items()):
new_cells.add((pos[0], pos[1]))The set new_cells contains the new iteration (or evolution) of The Game Of Life, given we have the old_grid.
In the first loop, we start by acquiring the live and dead neighbouring cells for each alive cell. We then check if the current live cell has either two or three neighbours, if not, we then remove that cell from the new grid – essentially killing it. This simultaneously implements both underpopulation and overpopulation rules.
Finally, in the first loop, we also add all the neighbouring dead cells of each live cell to a frequency count dictionary. More specifically, undead is a default dictionary of integers where the keys are the dead cell coordinates, and values are the number of live neighbours of that cell.
The icing on the cake is the second outer loop. For all the dead cells in undead, we filter out the cells that don’t have exactly three neighbours. For the remaining dead cells with three neighbours, we add the cell to the new grid, essentially birthing it.
Displaying The Game Of Life With A Graphics Library
For this task, I chose to use Pygame for the graphics engine. If you haven’t heard of it before, Pygame is a Python wrapper for the SDL graphics library, which is a C/C++ library that offers functionality to display graphics on many different platforms.
The setup for Pygame is actually very simple. In this section, we will learn how to initialise a graphics window, as well as the code for displaying our current grid on the screen!
Initialising Pygame’s Graphics Display
Unfortunately, graphics libraries like OpenGL, Vulkan and SDL are notorious for having a lot of boilerplate initialisation code. However, Pygame does all that work for us in the background, so the only code you need to initialise a graphics display window is the following.
import pygame
pygame.init()
window = pygame.display.set_mode((600, 400))Long story short, the code above initialises the graphics engine and creates a 600x400 display window, where the game will display. I chose 600x400px as it should be small enough for any monitors out there.
Displaying Conway’s Game Of Life Grid
With a display window, displaying the cells is actually quite easy. Fortunately, we can think of the Game Of Life grid as a bunch of equally spaced rectangles. To simplify things further, we can simply not draw the dead cells, only “painting” the live cells in the correct positions.
def draw_grid(window: pygame.Surface, grid: Grid) -> None:
cell_width = window.get_width() / grid.dim.width
cell_height = window.get_height() / grid.dim.height
border_size = 2
for (x, y) in grid.cells:
pygame.draw.rect(window,
(255, 0, 0),
(x * cell_width + border_size, y * cell_height +
border_size, cell_width - border_size, cell_height - border_size))Interestingly, the code above calculates each cell’s width and height from the Pygame window, then for each alive cell, we draw a red rectangle on the correct position.
The actual position depends on the cell’s coordinate, and to make things a bit prettier, we also draw the live cells a little smaller so there’s an empty “border” between them. I’ll let you figure out the maths!
The Code In Github
Most of the code was fairly well explained in this post. However, that is not the whole picture.
You can view the entire code in the Github repository I created for Conway’s Game Of Life in Python. More importantly, have a look at the file pygame_life.py , where the main logic of the game is, and the file grid_defs.py where all the definitions (such as Grid) are located.
I’d recommend looking at the main game loop in the main() function, that’s where all the code will be called from, as well as changing the current grid display in Pygame!
TL;DR – Implementing Conway’s Game Of Life In A Few Lines Of Python
By keeping it simple, and using the correct data structures, we can simplify the logic of the game quite a lot.
Always consider alternate implementations before choosing a final one. If you have time, see how each choice affects performance, memory use, and the readability of the code.
Creating graphics with Pygame is very straight-forward! Certainly much easier than the C/C++ counterparts.
At the time of writing, the whole Game Of Life implementation in the repo is about 77 lines long, which includes a nice initial Grid object for the gosper-glider setup (you can see it in the Github readme).
Have I missed anything? Do you have any questions or useful feedback? Feel free to comment below!
Be First to Comment